Use pythagorean theorem to find missing sides as follow:
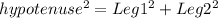
In triangle 1 frin the hypotunuse (MT) knowing that the legs are 3m and 13m:
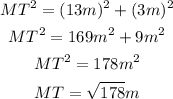
In triangle 2 find the hypotenuse (TL) knwing that the legs are 2m and 3m:
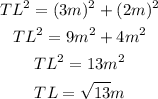
Add the lengths to get the perimeter:
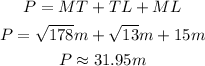
Then, the perimeter of the triangle MLT is (√178 +√13+15)m or approximately 31.95 m