Line AD bisecting ΔCAB results in two triangles. The first triangle ΔADB has angle measurements m_ADB = 100° and
m B = 48°. The total angle of a triangle is 180 degrees. Hence, the measurement of angle A on the triangle ΔADB is
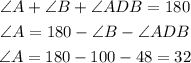
The triangle ΔCAD has no given angles on it. But we can find first the angle of m CDA by knowing that angle CDA and angle ADB as supplementary angles.

Using sine law, the angles DAB, CAD, BDA, and CDA are related as
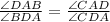
Solve for the value of angle CAD
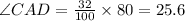
Hence, angle CAD has an angle measurement of 25.6°.