Given vertices have the next coordinates (x,y):
P(-6,2)
Q(3,2)
PART A: As the given vertices have the same y-coordinate, the distance is the difference between x-coordinates:
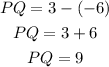
Then, the length of side PQ is 9 units
PART B: To find the area of the trinagle use the vertex R and vertex Q (they share the same x-coordinate) to find the height of the triangle:
The length of side QR is equal to the difference between y-coodinates of the vertices Q and R:
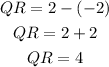
As you can see in the calculations above and in the image the length of he base of the triangle (side PQ) is 9 units, and its hight (Side QR) is 4 units; use the base and hight to find the area as follow:
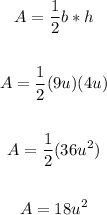
Then, the area of the given triangle is 18 square units