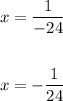Answer:
Step-by-step explanation:
Given the expression:
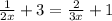
To solve this, first collect the like terms as:
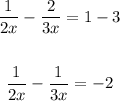
Next, we can multiply both sides of the equation by 6x to nullify the fractions on the left-hand side
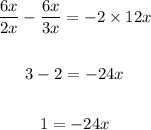
Finally, divide both sides by the coefficient of x, which is -24