Question

Please look at photo for accurate description round all sides to the nearest hundredth of a meter and round all the angle measures to nearest tenth

Answer 1

In order to calculate the length of the third side, let's use the law of cosines:

`\begin{gathered} b^2=a^2+c^2-2\cdot a\cdot c\cdot\cos (B) \\ b^2=8.32^2+5.97^2-2\cdot8.32\cdot5.97\cdot\cos (104.7\degree) \\ b^2=69.2224+35.6409-99.3408\cdot(-0.253758) \\ b^2=130.0718 \\ b=11.405 \end{gathered}`

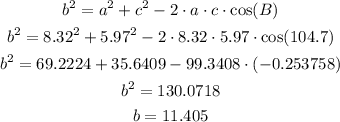
Now, let's calculate angle A using law of sines:

`\begin{gathered} (a)/(\sin A)=(b)/(\sin B) \\ (8.32)/(\sin A)=(11.405)/(0.9672677) \\ \sin A=(0.9672677\cdot8.32)/(11.405)=0.70562624 \\ A=\sin ^(-1)(0.70562624) \\ A=44.88\degree \end{gathered}`

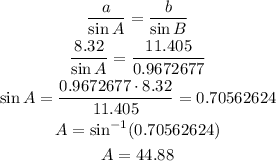
Since the sum of internal angles in any triangle is equal to 180°, we have:

`\begin{gathered} A+B+C=180 \\ 44.88+104.7+C=180 \\ 149.58+C=180 \\ C=180-149.58 \\ C=30.42\degree \end{gathered}`

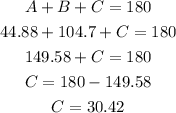
Therefore the answer is option A:

A = 44.9°, C = 30.4°, b = 11.41 m