Question

Use the empirical rule to answer each question during one week and overnight delivery company found the weight of its parent cells were normally distributed with a mean of 16 ounces in a standard deviation of 4 ouncesWhat percent of the parasails way between 8 ounces and 20 ounces Round your answer to one decimal placeWhat percent of the parasails weighed more than 8 ounces round your answer to two decimal places

Answer 1

Using the fact a normal distribution is symmetric and the empirical rules we can solve both questions. The empirical rules are:

1) 68% of the data falls within one standard deviation of the mean.

2) 95% of the data falls within two standard deviations of the mean.

3) 99.7% of the data falls within three standard deviations of the mean.

From the text, we know that the weight of the parent cells were normally distributed with a mean of 16 ounces with a standard deviation of 4 ounces

`\begin{gathered} \mu=16 \\ \sigma=4 \end{gathered}`

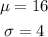
For the first question, we have the interval between 8 ounces and 20 ounces. Rewritting the limits of the interval as a function of the mean and standard deviation, we have

`\begin{gathered} 8=16-8=16-2(4)=\mu-2\sigma \\ 20=16+4=\mu+\sigma \end{gathered}`

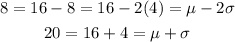
Then, our interval is

`(\mu-2\sigma,\mu+\sigma)`

If we combine the first two empirical rules, we know that between one standard deviation and two standard deviation falls the difference between 95% and 68% of the data.

`95\%-68\%=27\%`

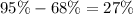
Since the distribution is symmetrical, we can divide it by 2 to find the data of the between one standard deviation and two standard deviation on one tail

`(27)/(2)=13.5`

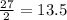
Adding this value to the first empirical rule, we have the result for our first question.

`13.5+68=81.5`

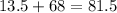
between 8 ounces and 20 ounces we have 81.5% of the parasails.

For the second question, we want to know the percent of data above 8 ounces.

From the second empirical rule, we know that 95% of the data falls within two standard deviations of the mean. If we divide this percentage by 2, we're going to find the amount of data between the mean and two standard deviations.

`(95\%)/(2)=47.5\%`

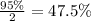
Since the distribution is symmetric, above the mean we have 50% of the area.

`47.5\%+50\%=97.5\%`

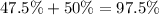
97.5% of the parasails weighed more than 8 ounces.