1 Answer

Nileshbirhade · Answer 1 · 2023-02-27T12:49:18+0000

We want to find the values of x and y. To do, we will use some trigonometric ratios to find their values.

Recall that given a triangle of this form

From this triangle we can define the following trigonometric ratios

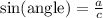
$\sin (\text{angle)}=(a)/(c)$
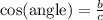
$\cos (\text{angle)}=(b)/(c)$
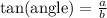
$\tan (\text{angle)}=(a)/(b)$

Using the angle of 45° as a reference, we can write

$\cos (45)=\frac{3\sqrt[]{2}}{x}$

Then, if we multiply both sides by x, we get

$x\cdot\cos (45)=3\sqrt[]{2}$

so, if we divide by cos(45) on both sides, we get

$x=\frac{3\sqrt[]{2}}{\cos (45)}$

Using that

$\cos (45)=\frac{\sqrt[]{2}}{2}$

we have that

$x=\frac{3\sqrt[]{2}}{\frac{\sqrt[]{2}}{2}}=\frac{3\cdot2\cdot\sqrt[]{2}}{\sqrt[]{2}}=6$

Now, we want to calculate the value of y. To do so, we can use the tangent as follows

$\tan (45)=\frac{y}{3\sqrt[]{2}}$

then multiplying both sides by 3*sqrt(2) we get

$\tan (45)\cdot3\cdot\sqrt[]{2}=y$

Using the fact that

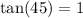
$\tan (45)=1$

we get that

$y=3\cdot\sqrt[]{2}\cdot1=3\sqrt[]{2}$

So, from this, we have that x=6 and y=3*sqrt(2)

Please log in or register to add a comment.