Question

Given the special right angle, find the value of x and y. Express your answer in simplest radical form.

Answer 1

We want to find the values of x and y. To do, we will use some trigonometric ratios to find their values.

Recall that given a triangle of this form

From this triangle we can define the following trigonometric ratios

`\sin (\text{angle)}=(a)/(c)`
`\cos (\text{angle)}=(b)/(c)`
`\tan (\text{angle)}=(a)/(b)`

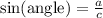
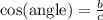
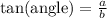
Using the angle of 45° as a reference, we can write

`\cos (45)=\frac{3\sqrt[]{2}}{x}`

Then, if we multiply both sides by x, we get

`x\cdot\cos (45)=3\sqrt[]{2}`

so, if we divide by cos(45) on both sides, we get

`x=\frac{3\sqrt[]{2}}{\cos (45)}`

Using that

`\cos (45)=\frac{\sqrt[]{2}}{2}`

we have that

`x=\frac{3\sqrt[]{2}}{\frac{\sqrt[]{2}}{2}}=\frac{3\cdot2\cdot\sqrt[]{2}}{\sqrt[]{2}}=6`

Now, we want to calculate the value of y. To do so, we can use the tangent as follows

`\tan (45)=\frac{y}{3\sqrt[]{2}}`

then multiplying both sides by 3*sqrt(2) we get

`\tan (45)\cdot3\cdot\sqrt[]{2}=y`

Using the fact that

`\tan (45)=1`

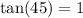
we get that

`y=3\cdot\sqrt[]{2}\cdot1=3\sqrt[]{2}`

So, from this, we have that x=6 and y=3*sqrt(2)