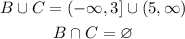In the picture we have a plot of the sets B (in blue) and C (in red).
We can write the sets in the interval notation:
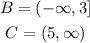
Q) We want to calculate the union and the intersection of those sets.
A)
1) B U C = union of B and C
The union of B and C sets are all the elements that belongs to B or C. Using the sets written in interval notation we see that:
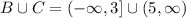
2) B ∩ C = insersection of B and C
The inserction of B and C sets are all the elements that belongs to B and C at the same time. From the graph of above we see that there are not elements that belongs to B and C at the same time, so the inserction does not has any elements, so the intersection of the sets is the emphy set (∅):
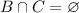
So, in summary the answer is: