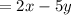Question

Reduce the following rational expression to its lowest terms.2x3 + x²y – 15xy2x² + 3xyAnswer

Answer 1

Given that,

`(2x^3+x^2y-15xy^2)/(x^2+3xy)`

To reduce the above rational expression to its lowest terms.

Consider the numerator,

`2x^3+x^2y-15xy^2`

Take x as common.

we get,

`=x(2x^2+x^{}y-15y^2)`

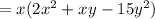
Put xy=6xy-5xy, to simplify,

`=x(2x^2+6xy-5xy-15y^2)`
`=x(2x(x+3y)-5y(x+3y))`

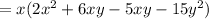
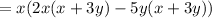
Taking x+3y as common we get,

`=x(x+3y)(2x-5y)`

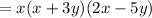
we get,

`=(x^2+3xy)(2x-5y)`

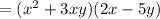
Substitute for numerator we get,

`(2x^3+x^2y-15xy^2)/(x^2+3xy)=((x^2+3xy)(2x-5y))/(x^2+3xy)`

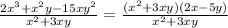
Cancelling the common term in the numerator ane denominator, we get

`=2x-5y`