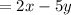Answer:
Given that,
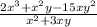
To reduce the above rational expression to its lowest terms.
Consider the numerator,
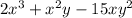
Take x as common.
we get,
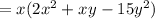
Put xy=6xy-5xy, to simplify,
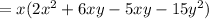
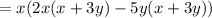
Taking x+3y as common we get,
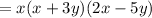
we get,
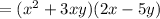
Substitute for numerator we get,
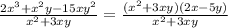
Cancelling the common term in the numerator ane denominator, we get