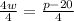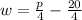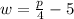The equation for its perimeter is P = 4w + 20
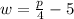
Step-by-step explanation
Let l represent the length of a rectangle and w represent the width of a rectangle.
Let p represent the perimeter of a rectangle.
From the given question, we first need to translate the statement into an equation.
If the rectangular pool's length is 10 feet longer than its width, then we can write the length of the rectangular pool as;
l = w + 10
The formula for calculating the perimeter of a rectnagle is given by the formula;
P = 2l + 2w
Substitute l = w + 10 into the above equation.
P = 2(w + 10) + 2w
Open the parenthesis.
P = 2w + 20 + 2w
Simplify.
P = 2w + 2w + 20
P = 4w + 20
Hence, the equation for its perimeter is P = 4w + 20
Next, is to solve for its width.
From the equation;
P = 4w + 20
Subtract 20 from both-side of the equation.
P - 20 = 4w + 20 - 20
p - 20 = 4w
Divide both-side of the equation by 4.