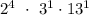Question

Find the prime factorization of following number. Write any repeated factors using exponents 624

Answer 1

The number 624 is composite and therefore it will have prime factors. Now let us learn how to calculate the prime factors of 624. The first step is to divide the number 624 with the smallest prime factor, here it is 2. We keep dividing until it gives a non-zero remainder.

624 ÷ 2 = 312

312 ÷ 2 = 156

156 ÷ 2 = 78

78 ÷ 2 = 39

Further dividing 39 by 2 gives a non-zero remainder. So we stop the process and continue dividing the number 39 by the next smallest prime factor. We stop ultimately if the next prime factor doesn't exist or when we can't divide any further.

Then, the prime factors of 624 are 2, 3, 13, and we have that the prime factorization of 624 is:

`2^4\text{ }\cdot\text{ }3^1\cdot13^{1^{}}`

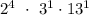
So that, we can conclude that the solution is:

`2^4\text{ }\cdot\text{ }3^1\cdot13^{1^{}}`