Question

Ron jeans and sneakers emperium Had 75 customers. 35 bought a pair of jeans, 45 boy sneakers and 20 bought sneakers and jeans. What is the probability a customer bought jeans or sneakers

Answer 1

4/5

1) Considering that Ron Jeans and Sneakers

75 customers

35 a pair of jeans

45 bought sneakers

20 bought Sneakers and Jeans

2) Now let's find out the subspace. The sum of all customers is 75. This is going to be the denominator.

Since the Question is about the Probability of a customer bought Jeans Or Sneakers. This is the same as the Union of the sets Sneakers and Jeans. So let's write out:

`P(AUB)\text{ =P(A) +P(B) -P(A}\cap B)`

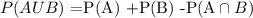
So P(AUB) is going to be the Jeans or Sneakers

P(A) = Probability of buying Jeans

P(B) = Probability of buying sneakers

P(A ∩B) = Probability of buying jeans And sneakers

Let's now plug into that, considering that there was a total of 75 customers:

`\begin{gathered} P(AUB)\text{ =P(A) +P(B) -P(A}\cap B) \\ P(AUB)\text{ }=(35)/(75)+(45)/(75)-(20)/(75) \\ P(AUB)=(60)/(75)=(4)/(5)\text{ or 0.8} \end{gathered}`

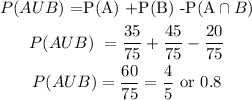
Note for each ratio we place the favorable outcomes over the total number of customers.

Hence, the answer is 4/5 or 0.8 The probability of buying jeans or sneakers in this sample of customers.