Question

Let f(x)=3x+4 and g(x) = x^2-6x+5Perform the function operation and then find the domain. f(x)•g(x)Simplify your answer.

Answer 1

the function is continuous so the domain is (-infinity, infinity).

Answer 2

Write out the function given

`\begin{gathered} f(x)=3x+4 \\ \text{and } \\ g(x)=x^2-6x+5 \end{gathered}`

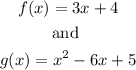
The operation is multiplication

Hence we multiply the two functions

`\begin{gathered} f(x)\text{.g(x)} \\ (3x+4)(x^2-6x+5) \\ \text{Expand the paranthesis} \\ 3x(x^2-6x+5)+4(x^2-6x+5) \end{gathered}`

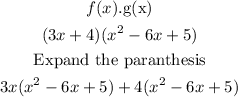
Then multiply each of the terms

`\begin{gathered} 3x(x^2-6x+5)+4(x^2-6x+5) \\ 3x^3-18x^2+15x+4x^2-24x+20 \\ \text{collect like terms and simplify } \\ 3x^3-18x^2+4x^2+15x^{}-24x+20 \\ 3x^3-14x^2-9x+20 \end{gathered}`

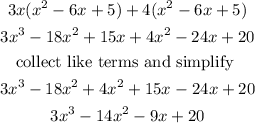
Hence

`f(x)\text{.g(x)}=3x^3-14x^2-9x+20`

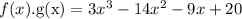
The domain of a function are the set of values of x for which the function is define or real

For the function f(x).g(x), there is no undefine point or domain constraint fpor the function,

hence

`\begin{gathered} \text{The domain is } \\ (-\infty,\infty) \end{gathered}`

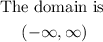
Therefore

f(x).g(x)= 3x³-24x²-9x+20

The domain is (-∞,∞)