SOLUTION
Write out the function given
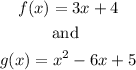
The operation is multiplication
Hence we multiply the two functions
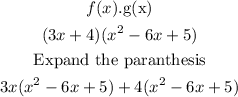
Then multiply each of the terms
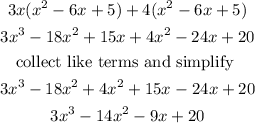
Hence
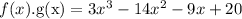
The domain of a function are the set of values of x for which the function is define or real
For the function f(x).g(x), there is no undefine point or domain constraint fpor the function,
hence
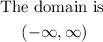
Therefore
f(x).g(x)= 3x³-24x²-9x+20
The domain is (-∞,∞)