Question

the area of a triangle is 27 . two of the lengths are 8.2 and 7.9 and the included angle is obtuse. Find the measure of the included angle, to the nearest tenth of a degree.

Answer 1

The area of a triangle given two sides and an included angle is given by:

`A\text{ = }(1)/(2)\text{ x b x c x sin A}`

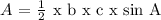
where a and b are the two sides given and A the included angle

so we can substitute to get the value for the included angle

Area, A = 27

b = 8.2

c = 7.9

`27\text{ =}(1)/(2)\text{ x 8.2 x 7.9 x sin A}`

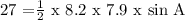
27 = 32.39 sin A

Divide both sides by 32.39

sin A = 27/32.39

sin A = 0.834

`\begin{gathered} A=\text{ }\sin ^(-1)0.834 \\ \\ A=56.5^0 \end{gathered}`

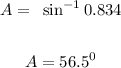
Also, since the angle is obtuse, then it falls within the second quadrant, then

the angle will be

`180^0-56.5^0=123.5^0`

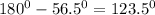
The included angle is 123.5