Step-by-step explanation:
Given;
We are given the linear equation below;
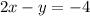
Required;
We are required to graph the equation of the line using the intercepts.
Step-by-step solution;
The graph of a line in standard form is given as;
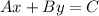
Note that the equation given already satisfies this condition. We can re-arrange the equation in the slope-intercept form which is;

We now have the following;

We can plot for at least 2 points by using the intercepts, that is when x = 0 and when y = 0;
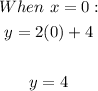
Also,
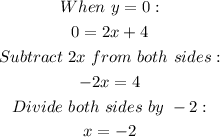
We now have the points;
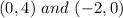
We can now plot these on a graph paper, and then extend the line at both ends. That is at the point where you have (-2, 0), we can draw the line continuously to the left and from the point where you have (0, 4), you can also draw the line continuously to the right.
With the aid of a graphing tool, the graph will come out like the one shown below;
ANSWER: