We want to get the value of r from the ratio test from the series;
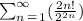
The ratio test is;
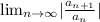
We can find the limit as;
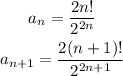
The quotient is; '

Therefore;
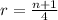
b. What does this value of r tell you about the series;
Taking the limit of the ratio r;
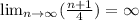
We can tell that the series is divergent.