Question

How do I classify the triangle? Is this an acute triangle

Answer 1

To classify this triangle we must find the values of the inner angles.

1) First, we find the value of x.

We know that the inner angles of a triangle sum 180°, so we have:

`\begin{gathered} (7x-11)\degree+(2x-3)\degree+(5x-2)\degree=180\degree, \\ 14x-16=180. \end{gathered}`

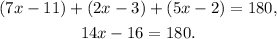
Solving for x the last equation, we get:

`\begin{gathered} 14x=180+16=196, \\ x=(196)/(14)=14. \end{gathered}`

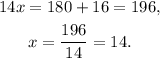
2) Using the value x = 14 we compute the values of the angles:

`\begin{gathered} a=(7\cdot14-11)\degree=87\degree, \\ b=(5\cdot14-2)\degree=68\degree, \\ c=(2\cdot14-3)\degree=25\degree. \end{gathered}`

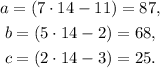
3) Because all the inner angles of the triangle are different and less than 90°, we have a scalene acute triangle.

Answer: scalene acute triangle