To classify this triangle we must find the values of the inner angles.
1) First, we find the value of x.
We know that the inner angles of a triangle sum 180°, so we have:
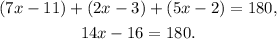
Solving for x the last equation, we get:
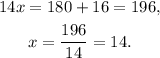
2) Using the value x = 14 we compute the values of the angles:
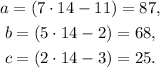
3) Because all the inner angles of the triangle are different and less than 90°, we have a scalene acute triangle.
Answer: scalene acute triangle