Question

Find the slope and y-intercept of the graph of the linear equation. Then write the equation of the line in slope-intercept form.

Answer 1

y=-3x-3

Step-by-step explanation

Step 1

find the slope of the line:

when you know 2 points of a line, P1 and P2, the slope is given by:

`\begin{gathered} \text{slope}=\frac{changein\text{ y }}{\text{change in x}}=(y_2-y_1)/(x_2-x_1) \\ \text{where} \\ P1(x_1,y_1) \\ P2(x_2,y_2) \end{gathered}`

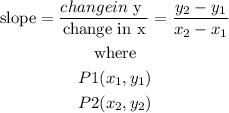
then, pick 2 coordinates of the line and replace

let

P1(0,-3)

P2(-1,0)

replace

`\begin{gathered} \text{slope}=(0-(-3))/(-1-0) \\ \text{slope}=(3)/(-1) \\ \text{slope}=-3 \end{gathered}`

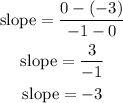
Step 2

find the y-intercept

the y intercept is the y value where the lines intersects the y axis

so, by checkin in the graph we have:

`\begin{gathered} y\text{ intercept=-3} \\ as\text{ ordered pair} \\ (0,-3) \end{gathered}`

Step 3

find the equation of the line:

a line can be expressed as

`y=mx+b`

where m is the slope and b is the y-intercept,this is called, slope intercept point form, then replace

`y=-3x-3`

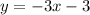
so, to check the y intercept, we can do

find y, when x= 0

`\begin{gathered} f(0)=-3(0)-3 \\ f(0)=0-3 \\ f(0)=-3 \\ (0,-3) \end{gathered}`

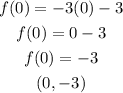
I hope this helps you