Question

A woodpecker’s brain is specially protected from large decelerations by tendon-like attachments inside the skull. While pecking on a tree, the woodpecker’s head comes to a stop from an initial velocity of 0.600 m/s in a distance of only 2.00 mm. (a) Find the acceleration in m/s2 and in multiples of g(g=9.80m/s2). (b) Calculate the stopping time. (c) The tendons cradling the brain stretch, making its stopping distance 4.50 mm (greater than the head and, hence, less deceleration of the brain). What is the brain’s deceleration, expressed in multiples of g?

Answer 1

Answers:

(a) a = -90 m/s² or 9.18g

(b) t = 0.00667 s

(c) a = -40 m/s² or 4.08g

Step-by-step explanation:

When the acceleration is constant, we can use the following equation:

`x=(1)/(2)(v_0+v_f)t`

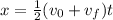
Where x is the distance, v0 is the initial velocity, vf is the final velocity and t is the time. So, replacing x by 2 mm (0.002 m), v0 by 0.6 m/s, and vf by 0 m/s, we can solve for t as:

`\begin{gathered} 0.002=(1)/(2)(0.6+0)t \\ 0.002=(1)/(2)0.6t \\ 0.002=0.3t \\ (0.002)/(0.3)=(0.3t)/(0.3) \\ 0.00667\text{ = t} \end{gathered}`

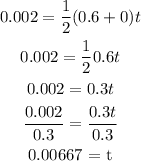
Therefore, the stopping time is 0.00667 s.

With this time we can calculate the acceleration using the following equation:

`a=(v_f-v_0)/(t)=(0m/s-0.6m/s)/(0.00667s)=-90m/s^2`

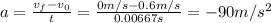
Then, to know the acceleration as a multiple of g, we need to divide 90 m/s² by 9.8 m/s² to get:

`(90)/(9.8)=9.18`

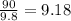
So, 90 m/s² is equivalent to 9.18g

In the same way, we can calculate the acceleration when the distance is 4.5 mm (0.0045 m). So, the stopping time is equal to:

`\begin{gathered} 0.0045=(1)/(2)(0.6+0)t \\ 0.0045=0.3t \\ (0.0045)/(0.3)=(0.3t)/(0.3) \\ 0.015\text{ s = t} \end{gathered}`

Then, the acceleration is equal to:

`a=(v_f-v_0)/(t)=\frac{0\text{ m/s - 0.6 m/s}}{0.015\text{ s}}=-40m/s^2`

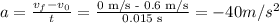
Since 40/9.8 = 4.08g, we can say that -40m/s² is equivalent to 4.08g.