We are given the equation of a parabola, and we are asked to find its vertex and axis of symmetry
The general form of a quadratic equation is the following

Written in this form, the point (h,k) represent the vertex of the parabola, that means that in the equation given by the problem
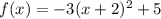
The vertex is the point
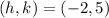
To find the axis of symmetry we need to expand the equation by solving the parenthesis and simplifying
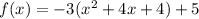

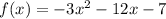
Written in this form, we have that the axis of symmetry is given by

where the coeficient b and a, come from the equation, knowing that the general form is the following

therefor, the axis of symmetry is equal to
