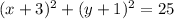
Step-by-step explanation
The equation of a circle with center (h,k) and radius r units is given by:
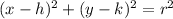
then
Step 1
find the diameter of the cirlce:
to do this, we can use the distance between two points formula:
if
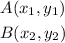
the distance from A to B is
![\begin{gathered} d_(AB)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rxwupk9jqyat885v9f8w0jiizyhf6vcbt7.png)
so,let
distance CD=
![\begin{gathered} CD=\sqrt[]{(1-(-7))^2+(2-(-4))^2} \\ CD=\sqrt[]{(8)^2+(6)^2} \\ CD=\sqrt[]{64+36} \\ CD=\sqrt[]{100} \\ CD=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/eedtjjr1ap6alb6olmoj0zl6z7wzwpe8ws.png)
hence, the diameter of the circle is

Step 2
find the center of the circle:
the center of the circle is the midpoint of CD
so
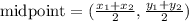
replace
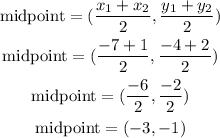
so, the center of the circle is (-3,-1)
Step 3
finally, replace in the formula to get the equation of the circle
let
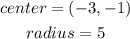
replace
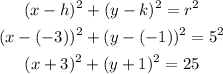
therefore, the answer is
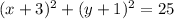
I hope this helps you