Question

I have to find measures of angles 1, 2, and 3 and then explain my reasoning using the different theorems such as corresponding angles theorem, alternate interior, alternate exterior theorem

Answer 1

Notice that angles 1 and the given angle with measure 68° are corresponding angles, therefore:

`\measuredangle1=68^(\circ).`

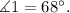
Now, angles 1 and 2 are alternate exterior angles, then:

`\measuredangle1=\measuredangle2=68^(\circ).`

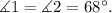
Finally, angles 2 and 3 are consecutive interior angles, then:

`\measuredangle2+\measuredangle3=180^(\circ).`

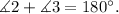
Solving for angle 3, we get:

`\measuredangle3=112^(\circ).^{}`

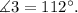
Answer:

Angle 1 is 68 degrees due to the corresponding angles theorem.

Angle 2 is 68 degrees due to the alternate exterior angles theorem.

Angle 3 is 112 degrees due to the consecutive angles theorem.

Examples:

Alternate exterior angles: angles A and B are alternate exterior angles.

Alternate interior angles: angles C and D are alternate interior angles: