(A) Let's find first the derivative of the function f(x), as follows:
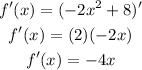
To find the slope of the line tangent to f(x), we just input x = 5 on the f'(x) to solve f'(5), which is:
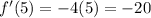
Hence, the slope of the tangent line is m = -20.
(B) The instantaneous rate of change is also the slope of the tangent line of the given function f(x). This means that it has the same value as part (A), which is f'(5) = -20.
(C) For the equation of the tangent line, let's look first at the tangent point. We can get this by substituting x = 5 on the equation f(x) and calculate:
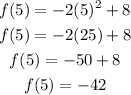
Our tangent point is (5, -48). We then use the slope-intercept equation y = mx + b to generate the equation of the tangent line.
We already solved m which is equal to -20. The values of x and y are equal to the tangent point. What's left is to compute the value of b. We substitute the values of m, x, and y on y = mx + b to solve b, as follows:
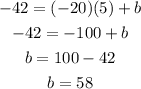
Hence, the equation of the tangent line can now be written as:

Answers:
(A) m = -20
(B) f(5) = -20
(C) y = -20x + 58