Let the distance travelled by Fernando to the meeting point, station, be 'x'.
Given that the distance between Fernando and Darrell is 43 kilometers, the distance between Darell and the station is (43-x) kilometers.
The schematic diagram is given below,
Consider the following relation,
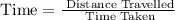
Given that the time talen by Fernando to cover 'x' kilometers at 59 km/hr is the same as the time taken by Davell to cover '43-x' kilometers at 77 km/hr,

Solve for the time taken to meet as,
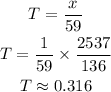
Thus, it took approximately 0.316 hours for both of them to meet.