Given the equation:
![(dy)/(dt)=\frac{y+1}{2\sqrt[\placeholder{⬚}]{t}}](https://img.qammunity.org/2023/formulas/mathematics/college/uoga1nbxyweyu1b68m1z5l3c9wr6tg7e6f.png)
When t=1, y=3 (three percent of the ants are infected).
Replacing in the equation:
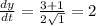
a) The equation of the line tangent to the graph is:
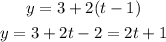
In t= 1.2.
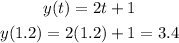
The percentage of the colony infected in t=1.2 is 3.4.
b) y explicity:
![\begin{gathered} (dy)/(dt)=(y+1)/(2√(t)) \\ \\ (dy)/(y+1)=\frac{dt}{2\sqrt[\placeholder{⬚}]{t}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8chkhbk3ztuqhgmsg3gid0fzt96be05s1f.png)
integrating both sides:
![\int(dy)/(y+1)=\int\frac{dt}{2\sqrt[\placeholder{⬚}]{t}}](https://img.qammunity.org/2023/formulas/mathematics/college/tz3s64karneuya1bav8s3j0qmcx0ijnxdh.png)
The first one will be:
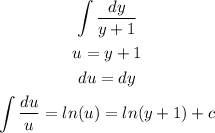
The second one, will be:
![\begin{gathered} (1)/(2)\int\frac{dt}{\sqrt[\placeholder{⬚}]{t}} \\ (1)/(2)\int t^{-(1)/(2)}dt=(1)/(2)*(\frac{t^{-(1)/(2)+1}}{-(1)/(2)+1})=(1)/(2)(\frac{t^{(1)/(2)}}{(1)/(2)})=t^{(1)/(2)}+k \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u7isghktew0l21uu0f3rc2r3rfcm8yx7yw.png)
Substituing:
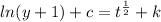
Using D=k-c
![\begin{gathered} ln(y+1)=t^{(1)/(2)}+D \\ y+1=e^{\sqrt[\placeholder{⬚}]{t}}*e^D \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nqr6yzqvgguad09v3a1w8zzn3hxhubxbn2.png)
Finally:
![y=e^{\sqrt[\placeholder{⬚}]{t}}e^D-1](https://img.qammunity.org/2023/formulas/mathematics/college/f061tpl7y6s1r8hdrztijl8yxlkiw7r006.png)