Given the unitary circle equation centered at the origin:
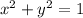
If the circle is not centered at the origin, but at the point (h, k), the equation becomes:

When h = k = 0, we have the particular case of a circle centered at the origin. Now, if the circle is not unitary, the equation becomes:
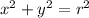
So when the radius is 1 (unitary circle), we have our initial case. Combining these results, the general equation of a circle of radius r and centered at (h, k) is:

r is always positive because it represents the measure of the radius length, and the length is always positive. On the other hand, the equation always represents a positive value, because the square of any number is always positive (or zero).