Let the amount of antifreeze be represented as X
The first brand is 45% pure antifreeze, this implies
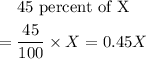
The second brand is 70% pure antifreeze, this implies
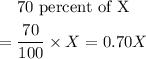
Since 50 gallons of the mixture contains 65% pure antifreeze, this implies
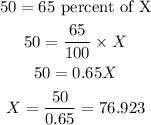
Thus, the amount of antifreeze is 76.923.
To determine the amount of antifreeze in each brand, we have
First brand:
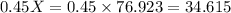
Second brand:
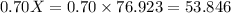
Hence, the first and second brands contain 34.615 and 53.846 gallons of antifreeze respectively.