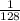Question

Suppose a single bacterium is placed in a bottle at 11:00 am. It grows and at 11:01 divides into two bacteria. These two bacteria each grow and at 11:02 divide into four bacteria, which grow and at 11:03 divide into eight bacteria, and so on. Now, suppose the bacteria continue to double every minute and the bottle is full at 12:00.How many bacteria are in the bottle at 11:53? What fraction of the bottle is full at that time?Question content area bottomThere will be   enter your response here bacteria in the bottle at 11:53(Type your answer using exponential notation.)part 2 how full will the bottle be?

Answer 1

Given:

A single bacterium is placed in a bottle at​ 11:00 am.

It grows and at​ 11:01 divides into two bacteria.

These two bacteria each grow and at​ 11:02 divide into four​ bacteria.

These four bacteria each grow and at​ 11:03 divide into eight bacteria.

The bottle is full at​ 12:00.

To find:

The number of bacteria are in the bottle at ​11:​53 and the fraction of the bottle is full at that​ time.

Step-by-step explanation:

After 1 min, the number of bacterias is,

`2^1`

After 2 min, the number of bacterias is,

`2^2`

After 3 min, the number of bacterias is,

`2^3`

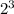
In general,

After t min, the number of bacteria is,

`2^t`

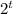
If the bottle is full at 12:00 that means after 60 mins, then the number of bacteria is,

`2^(60)`

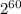
Therefore, the number of bacteria at 11:53 is,

`2^(53)`

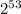
Then the fraction of the bottle is full at 11:53 is,

`\begin{gathered} \frac{Number\text{ of bacteria at 11:53}}{Total\text{ number of bacteria}}=(2^(53))/(2^(60)) \\ =2^(53-60) \\ =2^(-7) \\ =(1)/(2^7) \\ =(1)/(128) \end{gathered}`

Final answer:

• The number of bacteria at 11:53 is,

`2^(53)`

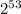
• The fraction of the bottle is full at 11:53 is,

`(1)/(128)`