Question

Which of the following are not trigonometric identities? Check all that app

Answer 1

Test each of the options to get those that are not a trigonometry identites

For option A

`\begin{gathered} \text{tanxcosxcscx}=1 \\ \tan x=(\sin x)/(\cos x) \\ \csc x=(1)/(\sin x) \end{gathered}`
`\tan x\cos x\csc x=(\sin x)/(\cos x)*\cos x*(1)/(\sin x)=(\sin x*\cos x)/(\cos x*\sin x)=1`

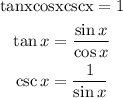
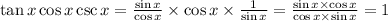
OPTION A IS A TRIGONOMETRY IDENTITY

For option B

`\begin{gathered} 1-\tan x\tan y=(\cos (x+y))/(\cos x\cos y) \\ \tan x=(\sin x)/(\cos x) \\ \tan y=(\sin y)/(\cos y) \end{gathered}`
`\begin{gathered} 1-\tan x\tan y=1-(\sin x)/(\cos x)*(\sin y)/(\cos y) \\ =1-(\sin x\sin y)/(\cos x\cos y) \\ =(\cos x\cos y-\sin x\sin y)/(\cos x\cos y) \end{gathered}`

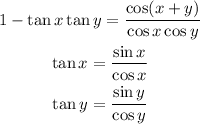
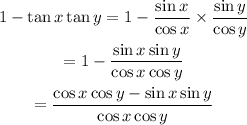
Therefore,

`(\cos x\cos y-\sin x\sin y)/(\cos x\cos y)=(\cos (x+y))/(\cos x\cos y)`

Multiply through by the common base

`\cos x\cos y-\sin x\sin y=\cos (x+y)`

The above expression is a trigonometry identity, so it is true.

OPTION B IS A TRIGONOMETRY IDENTITY

Checking for option C

`\begin{gathered} (\sec x-\cos x)/(\sec x)=\sin ^2x \\ (\sec x)/(\sec x)-(\cos x)/(\sec x)=\sin ^2x \\ 1-\cos x((1)/(\sec x))=\sin ^2x \\ \text{note} \\ (1)/(\sec x)=\cos x,\text{then} \\ 1-\cos x(\cos x)=\sin ^2x \\ 1-\cos ^2x=\sin ^2x \end{gathered}`
`1=\sin ^2x+\cos ^2x`

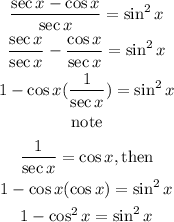
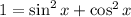
The above is a triogonometry identity

OPTION C IS A TRIGONOMETRY IDENTITY

Checking for option D

`4\cos x\sin x=2\cos x+1-2\sin x`

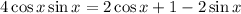
The above is not a trigonometry identity

OPTION D IS NOT A TRIGONOMETRY IDENTITY

Hence, the option that is not a trigonometry identity is OPTION D