We are given the following two equations
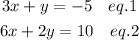
Let us solve the system of equations using the substitution method.
Separate out one of the variables in any of the two equations
Let us separate out x from eq.1
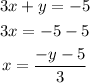
Now, substitute this value of x into eq.2

The variable y also got canceled and we are left with something that cannot be true. (-10 cannot be equal to 10)
This means that the system of equations has infinitely many solutions.