We have to identify the parabola that:
a) has no real solutions (it has complex roots).
b) opens downward.
The equations are in vertex form, so to have no real solutions and be downward, the vertex should have a value of y that is less than 0:
If the vertex had a value of y greater than 0, if it opens downward, there should be two values of x so that f(x) = 0. Then, this would be the real solutions.
The vertex form can be written as:
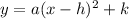
where (h,k) are the coordinates of the vertex.
Then, we need k <= 0.
The equations that satisfy this are:
y = -(x + 4)² - 2
y = -x² - 2
y = -(x - 4)² - 2
The second condition is that the parabola opens downward. This means a quadratic coefficient "a" with negative value.
All this three equations satisfy this condition.
We can graph them and check if the conditions are satisfied:
Answer:
There are 3 equations that satisfy the two conditions:
y = -(x + 4)² - 2
y = -x² - 2
y = -(x - 4)² - 2