Question

the cost of manufacturing and selling x units of a product is c-7x+11 and the corresponding revenue R is R - x^2 - 15 find the number of the units needed to earn below and above the btrak even value

Answer 1

We know:

Profit = Revenue - Cost

When Revenue is equal to Cost, we have the break-even point.

Let's equate revenue and cost:

`\begin{gathered} R=C \\ x^2-15=7x+11 \end{gathered}`

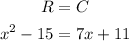
To find the value of x, we can take all terms to LHS (Left-Hand-Side) and use the quadratic formula. The process of finding x is shown below:

`\begin{gathered} x^2-15=7x+11 \\ x^2-15-7x-11=0 \\ x^2-7x-26=0 \\ u\sin g\text{ quadratic formula,} \\ x=-2.7,9.7 \end{gathered}`

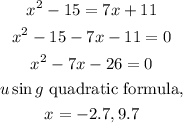
We can't have a negative value, so we disregard x = -2.7

What we have is

x = 9.7

So,

For 10 units (and above) sold, we will have a profit.

For 9 units (and below) sold, we will incur a loss.