The area of a circle is given by the following formula:
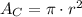
where r is the lenght of the circle's radius.
In this case, we have a radius of 12 units, so the area will be
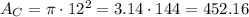
We are however, asked to find the area of the shaded region, which is encased within a square. From the image we can see that the circle's radius is half the length of a side of the square. In other words, the square's sides measure 24 units.
The area of a square is given by
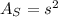
where s is the lenght of the sides of the square. In this case,
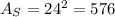
Now, in order to determine the area of the shaded region, we subtract the area of the circle from the area of the square:
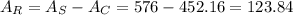
So the area of the shaded region is 123.84 square units.