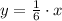For two numbers to be proportional, they must verify:
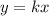
"y is proportional to x"
In this case, to verify this, we nedd to calculate if each value of y can be founded by multiplying x by a constant k.
If y = kx is true, then:
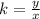
And if k is the same for al pairs (x, y) then the relationship is proportional.
Using the table we do:
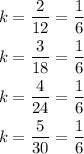
Since k is the same for all pair of values, y is proportional to x.
Also we have already calculated k = 1/6
And the equation that represents the table is: