Question

For an arch length s, area of sector A, and central angle θ of a circle of radius r, find the indicated quantity for the given valuer=55.8 cm, θ= pi\12 radians.

Answer 1

Hello!

First, let's write some important information:

• arch length,: s

,

• area of the sector,: A

,

• central angle θ,: π/12 rad

,

• radius r,: 55.8cm

To obtain the area of sector A, we must use the formula below:

`A=(r^2\cdot\theta)/(2)`

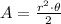
As we know some values, let's replace them:

`A=(55.8^2\cdot(\pi)/(12))/(2)=(3113.64\cdot(\pi)/(12))/(2)=((3113.64\pi)/(12))/(2)=(259.47\pi)/(2)=129.735\pi`

To finish, we must replace the value of π and solve the multiplication:

Note: I'll consider π = 3.1415 (approximated value).

`\begin{gathered} A=129.735\cdot\pi \\ A=129.735\cdot3.1415 \\ A\cong407.56 \end{gathered}`

The most approximated answer is alternative A. 407.575cm².