Question

How many photons are emitted during 3.5 s of operation of a red laser pointer? The device outputs 2.99 Watts at a 620.85 nm wavelength.

Answer 1

Given:

The power of the laser is P = 2.99 W

The time duration is t = 3.5 s

The wavelength of the laser is

`\begin{gathered} \lambda\text{ = 620.85 nm} \\ =620.85\text{ }*10^(-9)\text{ m} \end{gathered}`

Required: Number of photons emitted from the laser.

Step-by-step explanation:

The energy of the laser is given by the formula

`E=(nhc)/(\lambda)`

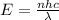
Here, n is the number of photons.

h is the Planck's constant whose value is

`h\text{ = 6.6}*10^{-34\text{ }}J\text{ s}`

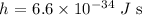
c is the speed of light whose value is

`c=3*10^8\text{ m/s}`

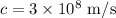
The energy can also be calculated as

`\begin{gathered} E=P* t \\ =2.99*3.5 \\ =10.465\text{ J} \end{gathered}`

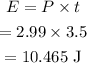
On substituting the values, the number of photons can be calculated as

`\begin{gathered} n=(E\lambda)/(hc) \\ =(10.465*620.85*10^(-9))/(6.6*10^(-34)*3*10^8) \\ =3.28*10^(19)\text{ } \end{gathered}`

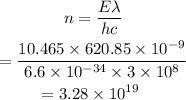
Final Answer: 3.28e19 photons are emitted.