SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the formula for area of a sector
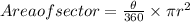
STEP 2: Write the given measures
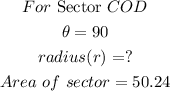
STEP 3: substitute the values in the formula in step 1
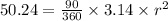
Solve for radius(r)
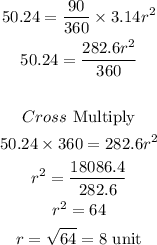
Therefore, the radius of the circle is 8 units
STEP 4: Calculate the measure of arc AB
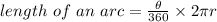
STEP 5: Write the known values
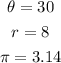
STEP 6: calculate the length of the arc
By substitution in to the formula in step 4, we have:
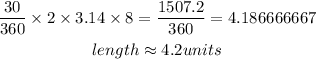
Hence, the measure of arc AB is approximately 4.2 units