Question

(10,1)(-10,3) what is the linear equation

Answer 1

y = -1/10 + 2

Step-by-step explanation:

To get equation of line: y = mx + c

m = slope

We will use the two points to find the slope

slope formula:

`m\text{ = }(y_2-y_1)/(x_2-x_1)`
`\begin{gathered} x_1=10,y_1=1,x_2=-10,y_2\text{ = }3 \\ m=(3-1)/(-10-10)=(2)/(-20)=(-2)/(20) \\ m\text{ = }-(1)/(10) \end{gathered}`

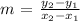
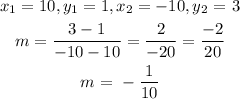
To get c, we need to use one of the points given:

Using point (10, 1) = (x, y)

1 = -1/10 (10) + c

1 = -1 + c

c = 1+1

c = 2

The linear equation becomes:

y = -1/10 + 2