y = -1/10 + 2
Step-by-step explanation:
To get equation of line: y = mx + c
m = slope
We will use the two points to find the slope
slope formula:
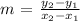
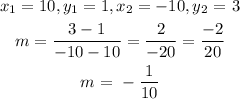
To get c, we need to use one of the points given:
Using point (10, 1) = (x, y)
1 = -1/10 (10) + c
1 = -1 + c
c = 1+1
c = 2
The linear equation becomes:
y = -1/10 + 2