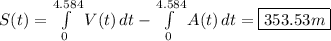Question

Calculator Active is given by V(t) = -31+50.5 Vaibhav and Alex walk in the same direction along a straight path. For 051310. Vaibhav's velocity at timet 6010 and Alex's velocity at time is given by Ad) = 8.57 1151 Both V (t) and A(t) are positive for Osts 20 and are measured in meters per minute. Vaibhav is 12 meters ahead of Alex at time =0. and Vaibhav remains ahead of Alex for 0(Need answers and precise)​

Answer 1

Hello!

a.

We can evaluate the integral using a calculator.

`(1)/(10)\int\limits^(15)_5 {V(t)} \, dt = 54.409 (m)/(min)`

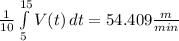
This integral is the equivalent of finding the average rate of change over a given interval:

`AROC = \frac{\int\limits^b_a {f(t)} \, dt }{b - a}` (A.K.A, the slope).

So, according to the solved value, Vaibhav walked at an average of 54.409 meters per minute.

b.

We can determine whether he is speeding up or slowing down by finding his ACCELERATION and whether it has the opposite sign as the velocity.

Use a calculator device to calculate the instantaneous acceleration at t = 10:

`(d)/(dt)V(10) = -7.036 (m)/(min^2)`

Now, find his velocity at t = 10 simply by plugging in 10 into V(t):

`V(10) = (6010)/((10^2) - 3(10) + 50.5) = 49.88 (m)/(min)`

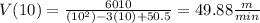
Since the velocity and acceleration are in OPPOSITE directions, Vaibhav is SLOWING DOWN at t = 10.

c.

An expression for the distance between the two can be found by subtracting the integrals of their respective velocity functions.

Let 'S' denote the distance between Vaibhav and Alex:

`S(t) = \int\limits^(20)_ {0}V(t)} \, dt - \int\limits^(20)_ {0}A(t)} \, dt`

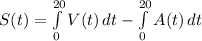
So, the change in their distance (velocity), is:

`S'(t) = V(t) - A(t)`

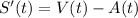
Evaluate at t = 18 using a device:

`S'(18) = V(18) - A(18) = 18.752 - 15.047 = 3.705(m)/(min)`

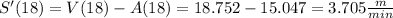
Since the difference in their velocities is positive, the distance between the two is INCREASING.

d.

We can find the maximum distance by evaluating S'(t) where there exists a maximum. (changes from + to -)

`0 = V(t) - A(t)\\\\V(t) = A(t)`

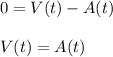
Solve using a graphing calculator, and we get:

`t = 4.584 \text{ min}`

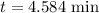
Now, find the maximum distance by subtracting the integrals:

`S(t) = \int\limits^(4.584)_ {0}V(t)} \, dt - \int\limits^(4.584)_ {0}A(t)} \, dt = \boxed{353.53 m}`