Question

Hi can you help me solve this equation to me so I can try to explain it to my daughter please

Answer 1

Given:

a.) He has 12 1/2 cups of milk.

b.) The chef has 3 1/2 more cups of broth than milk.

Step 1: Since it is said that the chef has 3 1/2 more cups of broth than milk, and he has 12 1/2 cups of milk, we will be adding 3 1/2 and 12 1/2 to get the actual number of cups of broth.

We get,

`\text{ 3 }(1)/(2)\text{ + 12}(1)/(2)`

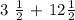
In adding mixed numbers, we add separately the whole numbers and fractions and add them together later on.

`\text{ 3 }(1)/(2)\text{ + 12}(1)/(2)\text{ = (Add whole numbers) + (Add fractions)}`
`\text{ = (3 + 12) + (}(1)/(2)\text{ + }(1)/(2))`
`\text{ = 15 + 1}`
`\text{ = 16 cups}`

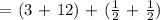
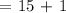
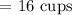
Therefore, the chef has 16 cups of broth.

Step 2: Let's now determine the remaining cups of broth after using 14 1/2 cups to make soup. We will be subtracting the current 16 cups of broth by 14 1/2 cups for the soup.

We get,

`\text{ 16 - 14}(1)/(2)`

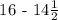
Let's first convert them into similar fractions before subtracting.

`\text{ 16 = }\frac{16\text{ x 2}}{2}\text{ = }(32)/(2)`
`\text{ 14}(1)/(2)\text{ = }\frac{(14\text{ x 2) + 1}}{2}\text{ = }\frac{28\text{ + 1}}{2}\text{ = }(29)/(2)`

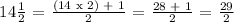
Let's now proceed in subtracting them,

`\text{ 16 - 14}(1)/(2)\text{ = }\frac{32}{2\text{ }}-\text{ }(29)/(2)\text{ = }\frac{\text{ 32 - 29}}{2}\text{ = }(3)/(2)\text{ or 1 }(1)/(2)\text{ cups}`

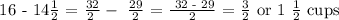
Therefore, the chef will have a remaining 1 1/2 cups of broths after using 14 1/2 cups for the soup.