Question

Consider a particle moving along the x-axis where x(t) is the position of the particle at time t, x' (t) is its velocity, and x'' (t) is its acceleration.

Answer 1

a) We have to find the speed x'(t) and the acceleration x''(t).

We can find them by deriving the expression for the position x(t), which is:

`x\left(t\right)=t^3-6t^2+9t-7`

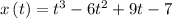
We can differentiate one time to find the speed:

`\begin{gathered} x^(\prime)\left(t\right)=3t^2-6\left(2t\right)+9\left(1\right)-7\left(0\right) \\ x^(\prime)\left(t\right)=3t^2-12t+9 \end{gathered}`

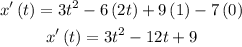
We can now differentiate one more time to find the acceleration:

`\begin{gathered} x^(\prime\prime)\left(t\right)=3\left(2t\right?-12\left(1\right)+9\left(0\right) \\ x^(\prime\prime)\left(t\right)=6t-12 \end{gathered}`

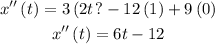
b) We have to find the intervals on which the particle is moving to the right.

This means that x(t) is increasing.

Knowing the speed function, the intervals where x(t) is increasing will match the intervals where the speed x'(t) is positive.

We have to also take into account that x(t) is defined only in the interval [0, 10]

Then, we can start by finding the roots of x'(t), as it is a quadratic equation:

`\begin{gathered} x=(-\left(-12\right?\pm√(\left(-12\right)^2-4*3*9))/(2*3) \\ x=(12\pm√(144-108))/(6) \\ x=(12\pm√(36))/(6) \\ x=(12\pm6)/(6) \\ x=2\pm1 \\ =>x_1=2-1=1 \\ =>x_2=2+1=3 \end{gathered}`

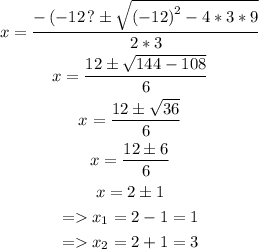
Then, we know that x'(t) changes sign at x = 1 and x = 3.

We can use the acceleration to check if the speed is increasing at x = 1 and, therefore, going from a negative value to a positive, or not:

`x^(\prime\prime)\left(1\right)=6\left(1\right)-12=6-12=-6`

The acceleration is negative at x = 1. This tells us that, as the speed is 0 at x = 1, it goes from a positive value to a negative value when crossing the axis.

Then, we can conclude that x'(t) is positive from x = 0 to x = 1.

Then, is negative from x = 1 to x = 3 and then again is positive from x = 3 to x = 10.

We then can write the interval where x is increasing (or moving to the right) as [0,1) U (3,10].

c) We have to find the speed when the acceleration is 0.

We start by finding the value of t for which the acceleration is 0:

`\begin{gathered} x^(\prime\prime)\left(t\right)=0 \\ 6t-12=0 \\ 6t=12 \\ t=(12)/(6) \\ t=2 \end{gathered}`

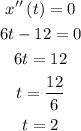
Then, knowing this happens at t = 2, we can calculate the speed at t = 2 as:

`\begin{gathered} x^(\prime)\left(2\right)=3\left(2\right)^2-12\left(2\right)+9 \\ x^(\prime)\left(2\right)=3*4-24+9 \\ x^(\prime)\left(2\right)=12-24+9 \\ x^(\prime)\left(2\right)=-3 \end{gathered}`

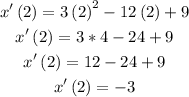
The speed, when the acceleration is 0, is .

Answer:

a) x'(t) = 3t² - 12t + 9

x''(t) = 6t - 12

b) [0,1) U (3,10]

c) -6