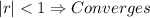A
1) The first thing to do, is to find the common ratio. So let's pick some terms and divide each one by its previous one to get the common ratio:
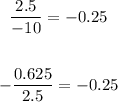
2) Now, let's take the absolute value of this ratio:
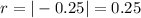
3) Based on that and analyzing the options, we can tell that: