Question

Find an equation for the given line in the form ax + by = C, where a, b, and care integers with no factor common to all three and a 20.Through (-8,20); parallel to 5x + 2y = 11The equation of the line in the form ax + by = c, passing through ( -8,20) and parallel to 5x + 2y = 11 is(Simplify your answer.)

Answer 1

In order to be parallel, the lines have to have the same slope.

When we have lines expressed in the form:

`ax+by=C`

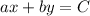
the slope has the value of the quotient:

`m=(-a)/(b)`

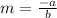
Then, if both lines have the same value for this quotient, both lines ahve the same slope. Therefore, they are parallel.

In our case, the slope of the parallel line is:

`m=(-a)/(b)=(-5)/(2)=-2.5`

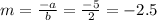
We will start by using the same values for a and b for our line. So a=5 and b=2.

Our line has to go through the point (-8,20).

We can use it to calculate C, in order to make the line go through this point.

We replace our equation with coordinates of the point and solve it for C:

`\begin{gathered} ax+by=C \\ 5x+2y=C \\ 5(-8)+2(20)=C \\ -40+40=C \\ C=0 \end{gathered}`

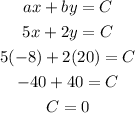
The equation of the line in the form ax + by = c, passing through ( -8,20) and parallel to 5x + 2y = 11 is 5x+2y=0