We need to find a function
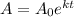
Suppose that t=0 corresponds to the year 4004BC; then
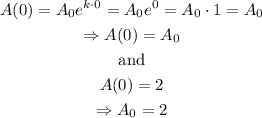
We need to find the value of k. The current year is 2022 and it corresponds to t=4004+2022=6026; then,
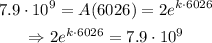
Solving for k,
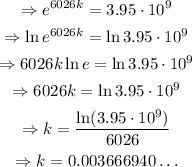
Then, the function is
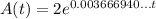
Evaluate for the year 2122, this is t=6126
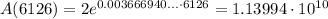
The population in 2122 will be, approximately, 1.14*10^10 people or 11.4 billion