In the circle with center E , DG and EF are tangents at point D and E respectively.
Therefore,

In quadrilateral DFEG ,
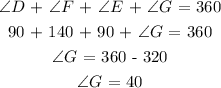
Now,
In the circle with center C , AG and BG are tangents at point A and B respectively.
Therefore,

In quadrilateral ACBG ,
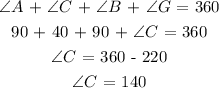
Thus the value of m